本文将介绍三个高级排序算法
- 希尔排序
- 归并排序
- 快速排序
希尔排序#
希尔排序(Shell’s Sort)的名称源于它的发明者Donald Shell,这是一种基于插入排序算法的改进。在处理大规模乱序数组时,插入排序的速度不容乐观,因为它只能一点一点的将元素从数组的一端移动到另一端。希尔排序为了加快速度,对插入排序进行了小幅的改动,开始时将数组划分为m相邻的若干个子数组,并对每一个子数组进行插入排序,然后缩小m的值再次划分并排序,循环往复直到完成m = 1时的最后一次插入排序,此时整个数组有序。
插入排序,每次将第k个元素插入前k-1个元素之间。
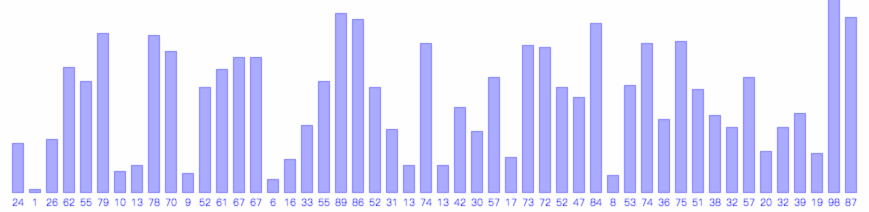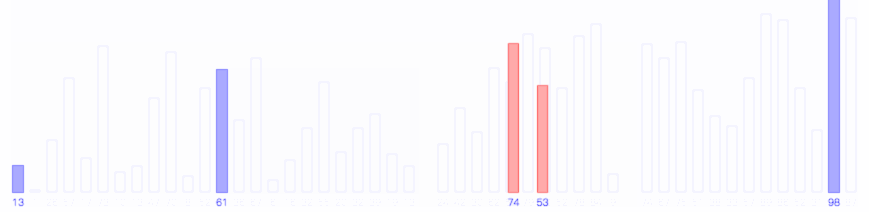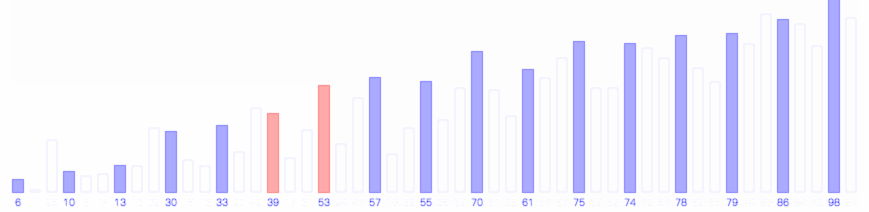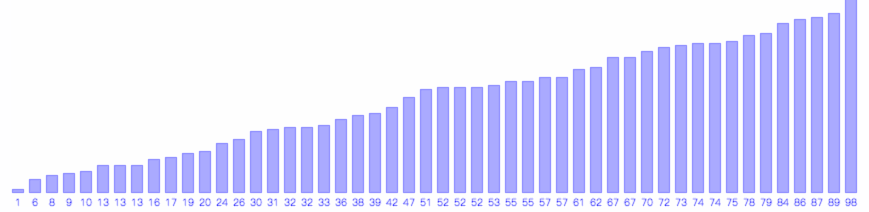
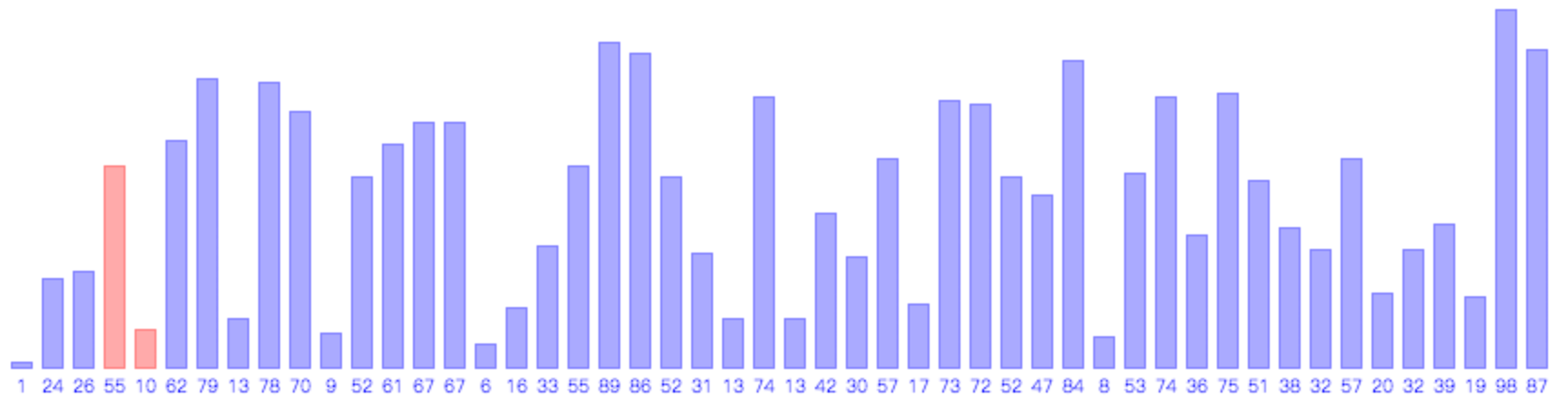 希尔排序示例,每次将第mk个元素插入到k,2k,3k…mk这m个元素之间。
希尔排序示例,每次将第mk个元素插入到k,2k,3k…mk这m个元素之间。
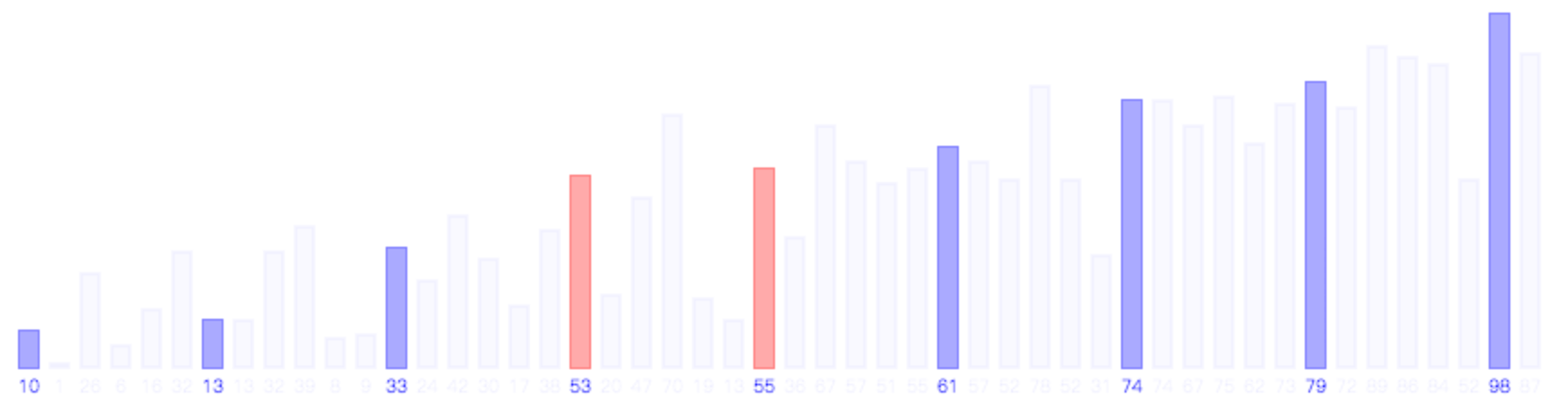
希尔排序的思路是使数组中任意间隔为m的元素都是有序的,这样的数组被称为m有序数组。一般m的初始值较大,以便我们可以将元素移动到很远的地方,随着希尔排序的进行,m会逐渐变小,当收敛到1时希尔排序完全退化为插入排序,从而完成最后的排序动作。
希尔排序高效的原因是它完全利用了插入排序的特点:
- 初始时,m值较大,子数组元素个数较小(小规模数据)
- 初始前几次,构造出了m有序子数组(部分有序)
希尔排序的过程如下图所示
希尔排序代码#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public static void shellSort(Integer arr[]) {
long before = System.currentTimeMillis();
int m = 1;
//获取的m值,与数组长度相关
//子数组的部分有序的程度取决于m的值,而如何选取m的值是一项数学难题,在这里我们采用`1 4 13 40 121 364`这样的序列来作为希尔排序中m的值。
while (m < arr.length / 3) m = 3 * m + 1;//1 4 13 40 121 364...
while (m >= 1) {//每轮循环结束时,m缩小3倍,直到收敛为1时,退化为插入排序
for (int i = m; i < arr.length; i++) {//从m开始
int temp = arr[i];//采用temp存放待插入元素
int j = i;
//取 arr[i],arr[i-m],arr[i-2m] ... 做插入排序
while (j >= m && temp < arr[j - m]) {
arr[j] = arr[j - m];
j -= m;
}
arr[j] = temp;
}
m = m / 3;
}
long after = System.currentTimeMillis();
System.out.println("希尔排序耗时:" + (after - before) + "ms");
}
|
与上一篇文章中的优化插入排序相比,希尔排序的优势还是很明显的。
20W条数据
插入排序耗时: 2776ms
希尔排序耗时: 25ms
归并排序#
归并排序的核心是归并操作,即将两个有序的数组合并为一个有序数组,归并过程如下所示
| 步骤 | sortedArr1 | sotedArr2 | resultArr |
|---|
| Init | 1 3 5 8 | 2 6 9 10 | - |
| Step1 | 1 3 5 8 | 2 6 9 10 | 1 |
| Step2 | 1 3 5 8 | 2 6 9 10 | 1 2 |
| Step3 | 1 3 5 8 | 2 6 9 10 | 1 2 3 |
| Step4 | 1 3 5 8 | 2 6 9 10 | 1 2 3 5 |
| Step5 | 1 3 5 8 | 2 6 9 10 | 1 2 3 5 6 |
| Step6 | 1 3 5 8 | 2 6 9 10 | 1 2 3 5 6 8 |
| Step7 | 1 3 5 8 | 2 6 9 10 | 1 2 3 5 6 8 9 |
| Step8 | 1 3 5 8 | 2 6 9 10 | 1 2 3 5 6 8 9 10 |
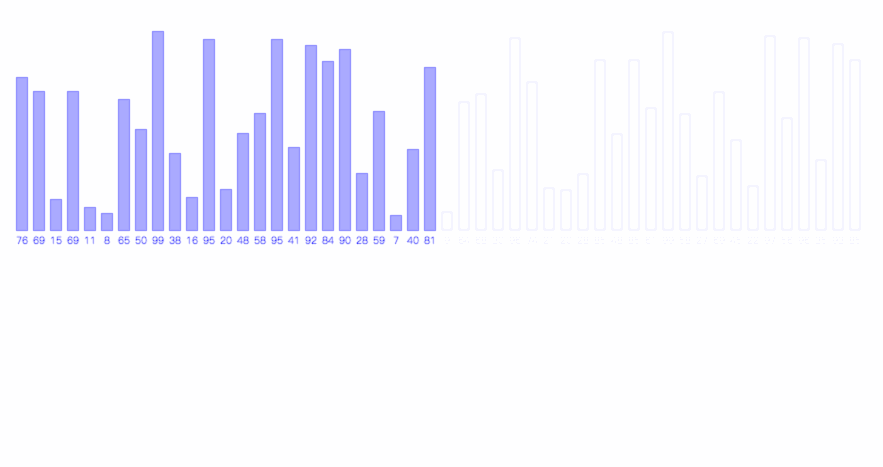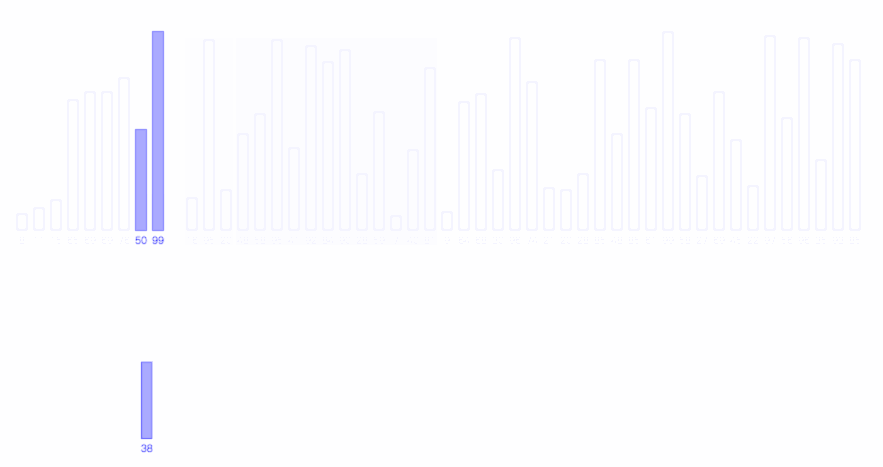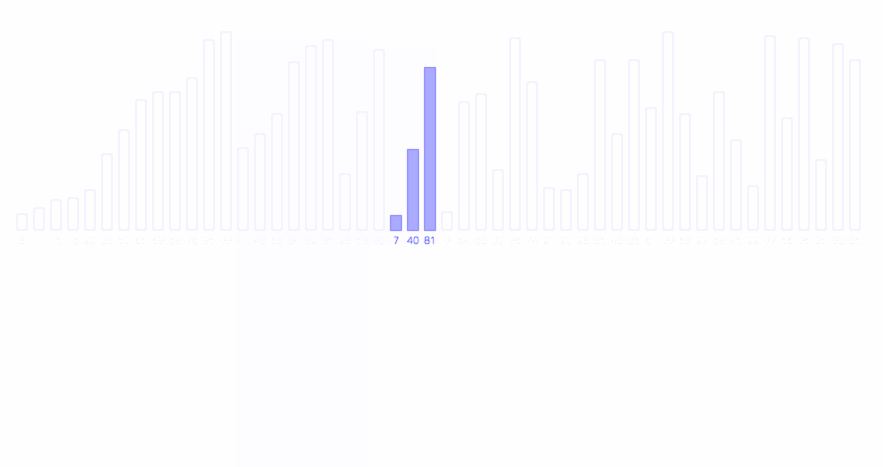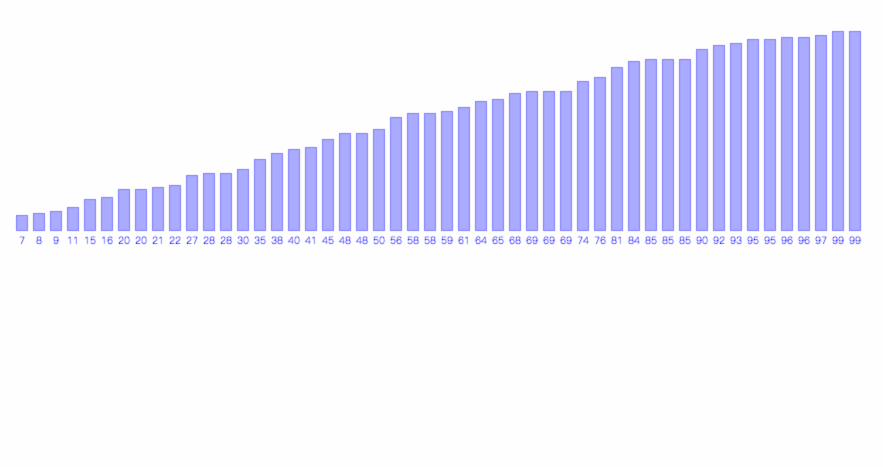
有了归并操作后,只需将待排序数组(递归地)划分为两半,直到每半只有一个元素时,便可将其视作有序的,从而将其合并为一个包含两个元素的有序数组,以此类推,最终将整个数组排序。

归并排序的过程如下图所示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public static void mergeSort(Integer arr[]) {
long before = System.currentTimeMillis();
mergeSort(arr, 0, arr.length - 1);
long after = System.currentTimeMillis();
System.out.println("归并排序耗时:" + (after - before) + "ms");
}
public static void mergeSort(Integer arr[], int low, int high) {
if (high <= low) return;
int mid = (low + high) / 2;
mergeSort(arr, low, mid);//将左半部分排序
mergeSort(arr, mid + 1, high);//将右半部分排序
merge(arr, low, mid, high);//对左右两个有序数组进行归并操作
}
public static void merge(Integer arr[], int low, int mid, int high) {
int i = low; //设i为左边有序数组的首索引
int j = mid + 1;//设j为右边有序数组的首索引
//将原数组先拷贝一份,在合并中使用
Integer aux[] = Arrays.copyOf(arr, arr.length);
for (int k = low; k <= high; k++) {
//若i的索引>mid,表明左边元素均已并入新的有序数组,此时只需将右边有序数组的剩余元素并入新的有序数组
if (i > mid) {
arr[k] = aux[j++];
} else if (j > high) {//若i的索引>mid,表明左边元素均已并入新的有序数组,此时只需将右边有序数组的剩余元素并入新的有序数组
arr[k] = aux[i++];
} else if (aux[j] < aux[i]) {//取左右有序数组中为并入新的有新数组中的的较小元素,将其并入到新的有序数组中
arr[k] = aux[j++];
} else {
arr[k] = aux[i++];
}
}
}
|
对于含有N个元素的数组,需要logN次划分,每次合并分别需比较2,4,…,N/4,N/2,N次。因此归并排序的时间复杂度为 $O(N*log_2 N))$
快速排序#
快速排序是应用最广泛的排序算法,在各SDK里边都有出现。与归并排序相似,快排也需要对原数组进行划分,然后对划分后的两个子数组单独的进行排序。不同的是,快排在划分时不是简单的二等分,而是与原数组有关。
快速排序步骤
- 取数组中的第一个元素的值作为参考值v
- 从前向后扫描,找到第一个比v大的元素,并记录其索引为i
- 从后向前扫描,找到第一个比v小的元素,并记录其索引为j
- 交换i和j的位置,分别从i和j的位置继续步骤2-3,直到
i>=j时结束扫描,并交换数组首元素与索引为j的元素。此时我们将开始时的首元素调整到的j的位置,且j之前的元素均比j小,j之后的元素均比j大。而j就是我们得到的划分位置。 - 以j为中心,将数组划分为两个子数组,分别重复步骤1-4。
快速排序的过程如下图所示,图的红线即为每次的划分时所用的参考值。
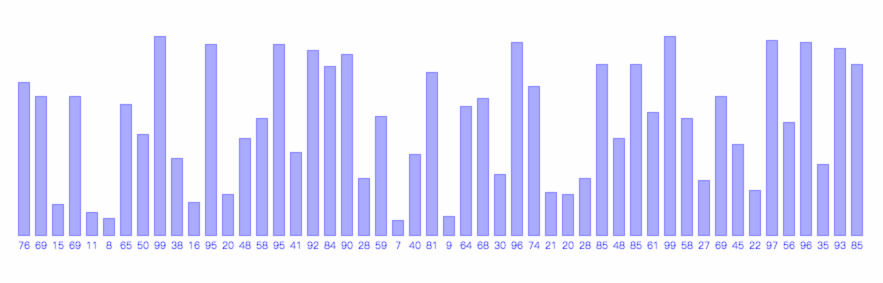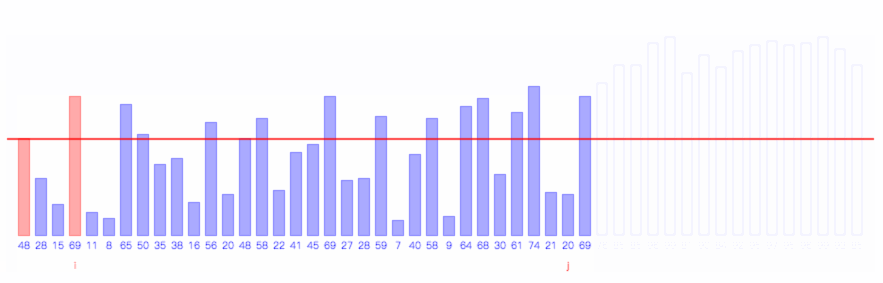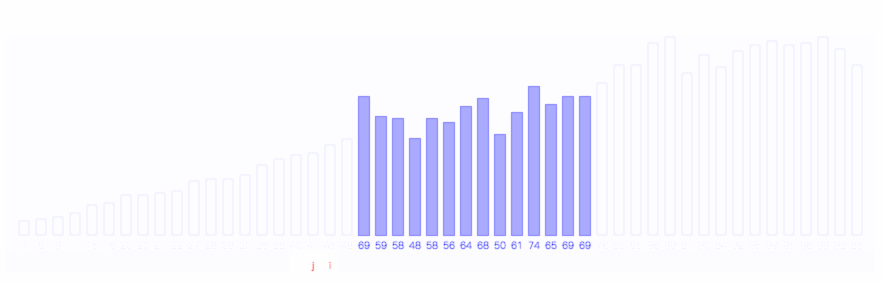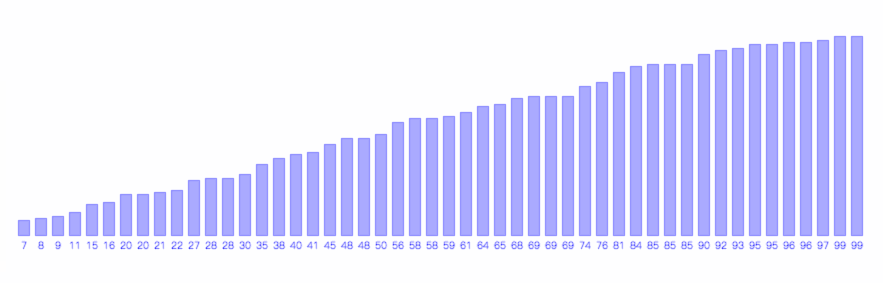
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| public static void quickSort(Integer arr[]) {
long before = System.currentTimeMillis();
quickSort(arr, 0, arr.length - 1);
long after = System.currentTimeMillis();
System.out.println("快速排序耗时:" + (after - before) + "ms");
}
public static void quickSort(Integer arr[], int low, int high) {
if (high <= low) return;
int j = partition(arr, low, high);//获取切分点
quickSort(arr, low, j - 1);//对左子数组进行排序
quickSort(arr, j + 1, high);//对右子数组进行排序
}
public static int partition(Integer arr[], int low, int high) {
int v = arr[low];//将首元素作为参考值
int i = low + 1;//记录当前数组的起点
int j = high;//记录当前数组的终点
while (true) {
while (arr[i] <= v && i < high) {
i++;//若arr[i]不大于v,则向后扫描
}
while (arr[j] >= v && j > low) {
j--;//若arr[j]不小于v,则向前扫描
}
if (i >= j) break;
swap(arr, i, j);
}
swap(arr, low, j);
return j;
}
|
以上所讲的三个排序算法中,都用到了划分这一操作。在算法学习中,我们把通过把大规模问题划分为小规模问题,分而治之的策略称为分治策略,也叫分治法。在分治法中经常会递归地求解一个问题,在每层递归中采用如下三个步骤:
- 分解:将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小
- 解决:递归的求解出子问题。如果子问题的规模足够小,则停止递归,直接求解
- 合并:将子问题的解组合成原问题的解
| 排序算法 | 问题规模(待排序元素个数) | 解题时间1 | 解题时间2 | 解题时间3 | 平均解题时间 |
|---|
| 希尔排序 | 10W | 30ms | 34ms | 32ms | 32ms |
| 快速排序 | 10W | 24ms | 23ms | 45ms | 30.6ms |
| 归并排序 | 10W | 4885ms | 4908ms | 4822ms | 4871.7ms |
| 希尔排序 | 50W | 174ms | 183ms | 196ms | 184.3ms |
| 快速排序 | 50W | 117ms | 124ms | 122ms | 121ms |
| 希尔排序 | 100W | 450ms | 434ms | 413ms | 432.3ms |
| 快速排序 | 100W | 217ms | 268ms | 235ms | 240ms |
 希尔排序示例,每次将第mk个元素插入到k,2k,3k…mk这m个元素之间。
希尔排序示例,每次将第mk个元素插入到k,2k,3k…mk这m个元素之间。




